du
tordage des courbes
(( Nouvelles astuces géométrie analytique))
On prend la surface dans l`espace cartésien Oxyz ,((voir le figure 1 :))
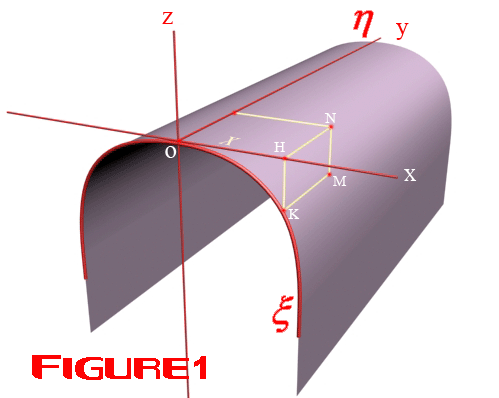
Soit le plan portant une courbe :
ou :
;
On imagine maintenant qu`on a tordu
parfaitement le plan qui est absolument mou
et inétirable,((ou indilatable )),sur cette surface de
sorte que s`applique sur Oy ,puis on fait
l`élévation verticale de cette courbe tordue sur le plan oxy ,
Alors quelle est l`équation cartésienne de la nouvelle courbe obtenue au oxy ?
Soit M un point de la surface précédente , dont
les cordonnées Cartésiennes sont (x,y) par
rapport au plan oxy,
et par rapport au plan tordu
C`est-à-dire: x=OH , y=NH ; et =l`arc( OK),
=l`arc(KM);
Et maintenant nous devons savoir la relation entre x et ,
et entre y et
:
D`abord on remarque facilement
que y=
Ensuite, on a :
=
Donc : , et
:
Exemple :
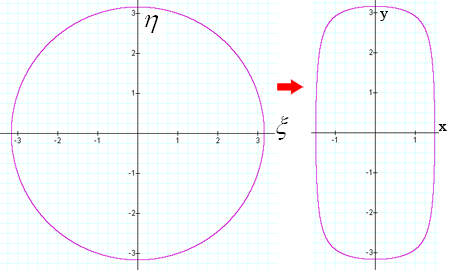
Soit le cercle : ,
tracé sur le plan
On le tord parfaitement sur la surface :
En appliquant sur oy,puis (( après le tordage)) on
fait l`élévation verticale sur le plan Oxy ,alors il se dessine sur Oxy la courbe
suivante :
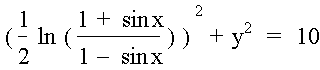
C`est-à-dire :il nous suffit de changer :
le en
; et
le
en y
C`est-à-dire :
f( )=0 -------
f(
,y)=0
La courbe d`origine La nouvelle courbe engendrée
· L`invers:
On a la courbe C : f(x,y)=0 dans le plan Oxy ,
mais le plan est
tordu parfaitement sur la surface
, ((voir
figure 1 )), on fait l`élévation
verticale de la courbe C , sur
tordu,puis on déploye le plan
pour se rend
un plan « non-tordu, » ;
Alors quelle est l`équation de la nouvelle courbe
obtenue ?
La solution : il nous suffit de changer :
,
et y en
,
C`est-à-dire :
f(x,y)=0 ----- f(
,
) = 0
Exemple : On imagine la courbe tracée
au plan oxy,faisons l`opération inverse expliquée
ci-dessus,on obtient alors la nouvelle courbe
suivante :
:
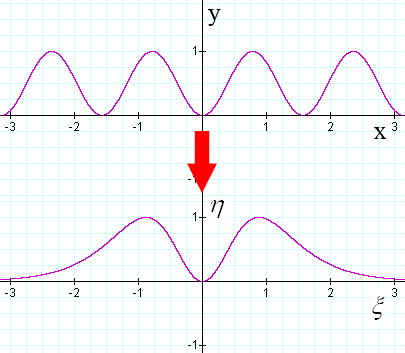
Remarquons
que est une ligne de convergence
De cette nouvelle courbe obtenue !
___________________________________________________________